The hardest computational problems

Computers can do more and more things remarkably well.¹ The days that humans can beat computers at chess are long gone and recently Go has suffered the same fate.^{2 3} With advancements in machine learning, computers are even getting better at less well defined tasks like image and voice recognition. But there are still tons of tasks that humans can do much better: cooking, programming, having a conversation, etc. So far, no computer comes close to passing the Turing test.

World chess champion Garry Kasparov was defeated by chess computer Deep Blue in 1997. Photo by Owen Williams.⁴

But in this post I want to look at a different kind of problems. Problems that are very well defined, such that they have a specific input and every specific input has an objectively correct answer. And from those we will consider only the problems that have a yes-no answer, these are what we call decision problems in computer science.⁵

Decision problems that take long to solve

In complexity theory a problem is called hard when it takes long on our computers to solve large instances of the problem. So then the longer it takes on large instances, the harder the problem would be.

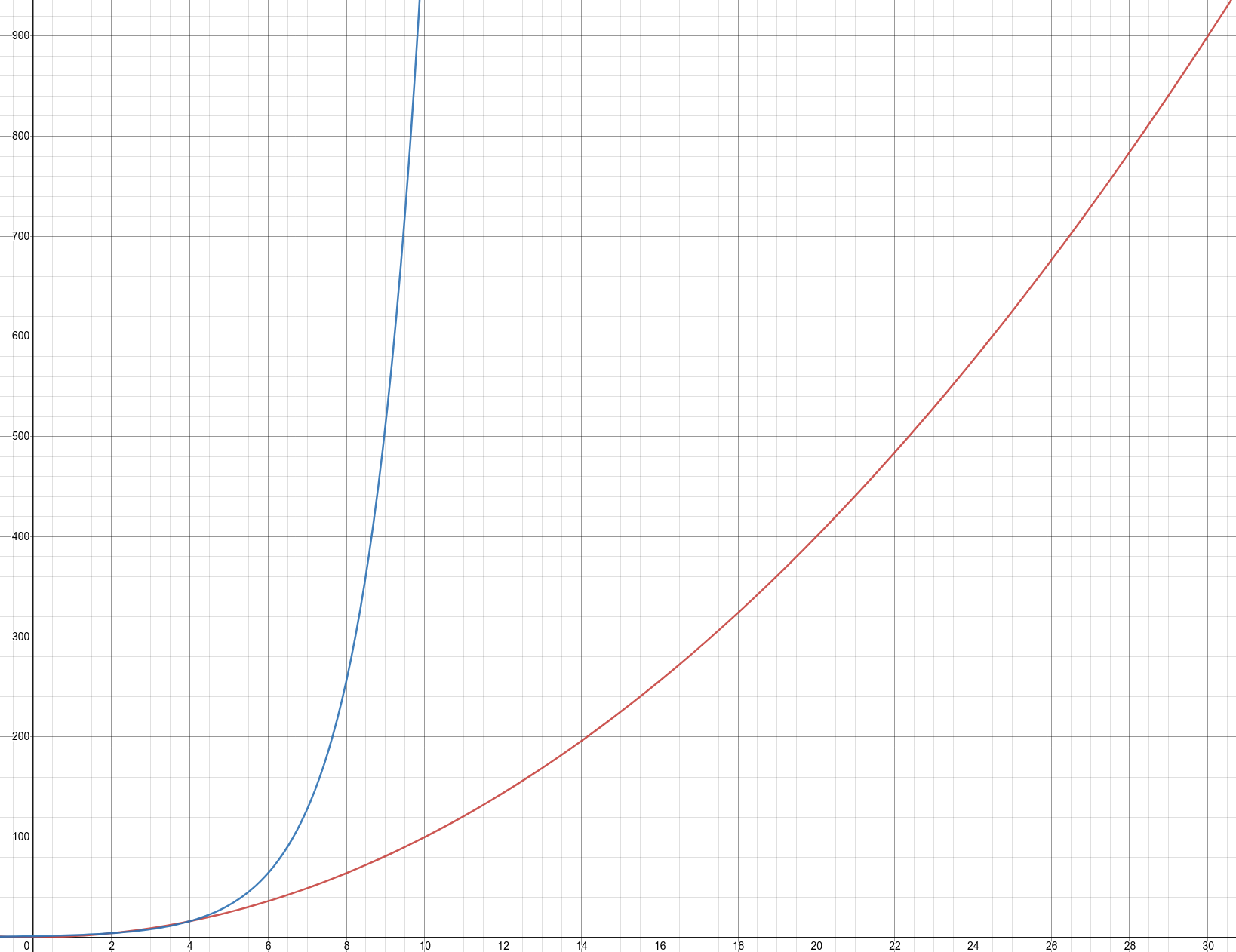
In the graph you can see that 2^x (blue) grows much quicker than x^2 (red) for large values.

If you have some computer science background, you might know about NP-hardness. If a problem is NP-hard, then there is no algorithm that can solve it in polynomial time if P≠NP.⁶ For example SAT, the problem of deciding if a given propositional formula is satisfiable, is NP-hard.

Such a problem that has no polynomial time algorithm is clearly harder than a problem in P, since it takes longer for our computers to solve that problem. And there is a whole wealth of complexity classes with problems that have different time and space needs for large input sizes. But all these problems can still be solved if we have enough time and space and we can do better than that. Let’s instead look at some unsolvable problems!

The halting problem

The halting problem is the problem of deciding whether a given computer program will eventually terminate. Some computer programs always terminate (examples in Python):

print("Hello world!")

So in the halting problem, when we are given this program, the correct answer is yes. But other programs will never terminate:

while True:
    print("I'm stuck")

This program will never exit its loop, so the correct answer is no. This might seem pretty straight forward, so why is this problem undecidable? When Turing proved this in 1936, computer science was just getting started, so he had to device a whole model for computation to proof this. However, the idea is suprisingly straight forward.

Suppose that the halting problem is decidable, then we should be able to make a function halts that takes a function and returns whether it halts in finite time. But then we can construct the following program:

def g():
    if halts(g):
        while True:
            print("I'm stuck")

Now consider g. If halts(g) returns True, then g never halts, which is in contradiction with the fact that halts is our halting function. If halts(g) returns False, then g does halt, but again this is in contradiction with the fact that halts is our halting function. So a halting function simply can’t exist and so the halting problem is not decidable.⁷

Alan Turing showed that the halting problem was undecidable in 1936

And it turns out there are many more problems that are undecidable, just like the halting problem.⁸ Some interesting examples are the Entscheidungsproblem and solving Diophantine equations. But are all unsolvable problems of the same caliber? Or are some harder then others?

Turing degrees

To answer this question, we are forced to further define what we mean with hard. Luckily, now we enter the realm of computability theory and here we have a whole hierarchy of just how unsolvable a problem is. We call this level of unsolvability the Turing degree of the problem and the higher it is, the harder the problem.^{9 10}

Rough sketch of the partial order of Turing degrees, with infinitely many Turing degrees missing (also between the different degrees).

The Turing degrees are defined through the concept of Turing reducibility. A problem X is Turing reducible to a problem Y if we can write a program that solves problem X if we get answers to problem Y for free.¹¹ Two problems have the same Turing degree if they are Turing reducible to each other and one Turing degree a is lower than a Turing degree b if all problems with Turing degree a are Turing reducible to a problem with Turing degree b. This means that if we can solve a problem with Turing degree n then we can solve all problems with Turing degree n or lower. So the higher the Turing degree, the harder the problem!

Obviously all computable problems are Turing reducable to all other problems, because we can already write a program to solve them, even if we don’t get the answers to any other problem for free. Because of this all the computable problems are in the lowest Turing degree, which we call 0. The halting problem has a Turing degree which we call 0’, which is strictly higher than 0, because we can’t solve the halting problem when we only get the answer to a computable problem.

Harder problems

So with our new definition of hardness, when we ask for a harder problem than the halting problem, we simply want to find a problem that we can’t solve even if we magically did have this halts function. So lets imagine we import some library that gives us this halts function, for any Python function we pass to halts it will tell us in finite time whether that function halts.^{12 13} Then what are the problems we still can’t solve?

We can use a similar argument as Turing did for the halting problem and define the halting^2 problem as deciding whether a given Python function that can use the halts function halts. Let’s assume that a function exists that solves this and we can define it using only ordinary Python and the halts function, we’ll call it halts2. Now we define the function h as:

from oracles import halts

def h():
    if halts2(h):
        while True:
            print("I'm stuck")

^{14 15}

But now we have the same paradox as before! So halts2 can’t be defined only using Python and halts. Which means that according to our definition of hardness, the halting^2 problem is harder than the halting problem. And we can keep doing this, defining halting^3, halting^4, etc. Each of them will be strictly harder than the previous.

So we run into the same problem that we get when someone asks us what the largest natural number is. There is no largest number, because for every natural number we are given, we can give a higher one. Similarly, there is no hardest problem, for any given hard problem, we can give a harder one.¹⁶ Still, this allows us to give some very hard problems, like halting^(10^10), halting^(googolplex) or halting^(BusyBeaver(googolplex)).¹⁷

Other Turing degrees

This halting trick doesn’t even give us all possible hard problems. It actually turns out that there are infinitely many other problems that are not Turing reducible to any of these ordinary halting problems and to which none of the halting problems are reducible.¹⁸ And all these problems have halting problems of their own, defined by the halting of computers that have access to their solutions, that are strictly harder. And then you have the infinitely many halting problems of these halting problems of these incomparable problems, each leading to very hard problems that are still incomparable with our ’normal’ halting problems through Turing reducibility.

The definition of hardness we use can’t say which of these problems is harder. Clearly they are different, but since neither is Turing reducible to the other, neither is harder than the other. But that makes sense, I don’t think there is any real way to compare the hardness of such problems.

Conclusion

The landscape of uncomputable decision problems is dauntingly huge. We have seen that there are much harder problems than just the halting problem and that there is no hardest problem. Next time you struggle to come up with the answer to a hard question you can console yourself with the idea that it could be much worse. They could have asked you to the decide the halting^1000 problem and we’ve seen how truly hard that is.